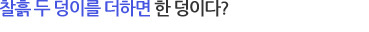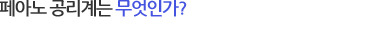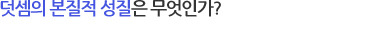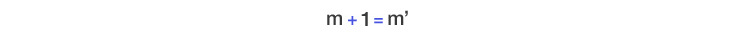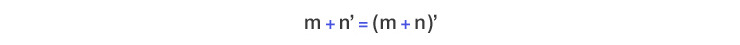왜 1+1=2를 증명하는 것이 어렵다는 소문이 난 것일까?

 

 

 

 

발명왕 에디슨이, “찰흙 한 덩이에 찰흙 한 덩이를 더하면 여전히 한 덩이이므로 1+1=1일 수도 있다”고 질문해서 선생님이 말문이 막혔다는 일화가 있다. 많은 사람들이 이 일화에 공감하는 것을 볼 수 있다. 에디슨은 오른손에 한 덩이를 들고, 왼손에 한 덩이를 든 다음, 두 덩이를 합쳐서 한 덩이라고 말을 했다는데 과연 에디슨의 말은 옳은 것일까? 곰곰이 생각해 보자.

 

 

 

 

 

에디슨이 오른손에 든 한 덩이와 왼손에 든 한 덩이는 같은 한 덩이일까? 정확히 무게를 재보고 부피를 재보거나 모양을 보면 틀림없이 다를 것이다. 양쪽이 다른 데도 같은 '한 덩이'라는 말을 쓴 것을 보면, 에디슨에게는 '한 덩이'란 '한 손으로 쥘 수 있는 양' 정도의 뜻이었을 것이다. 그럼 양손에 든 한 덩이씩을 합친 것은 한 손으로 쥘 수 있는 양일까? 아닐 것이다. 즉, 에디슨의 주장 1+1=1에서 등호 = 뒤에 나오는 1은 등호 앞에 나오는 두 개의 1에서와 뜻이 달라진 것이다. 따라서 에디슨의 주장은 사실이 아니다. 더구나 '한 덩이'는 사람마다 기준이 달라지는 '애매모호'한 단위라는 사실을 지적할 수 있다. 애매모호하지 않은 단위인 그램(g) 같은 것을 썼더라면 이런 잘못을 범하지는 않았을 것이다.

 

 

대부분의 사람은 1+1=2라는 사실을 알고 있고, 아마도 사람이 태어나서 가장 처음 배우는 '공식'일 것이다. 그런데 막상 이 공식이 왜 성립하는지 이유를 아느냐, 혹은 증명을 어떻게 하느냐고 물어보면 대부분의 반응은 두 가지로 나눌 수 있다.   1. 당연하잖아. 증명할 필요조차 없다. 2. 모르겠다. 증명이 어렵다고 들었다.

 

하긴 ‘3. 난 수학이 싫어.’나 ‘4. 그걸 왜 나한테 물어?’가 더 많을 것 같다. 어떻게 보면 아주 상반되는 반응인데 왜 이런 일이 생긴 것일까? 사실 1번의 반응을 보이는 사람이 많고, 실제로도 1+1=2인 이유는 당연하다고 말해도 무방할 정도로 간단하지만 그 '당연'한 얘기를 잠시 써 보자.    1, 2, 3, ...과 같은 자연수는 사람이 돌멩이 같은 사물의 개수를 세면서 자연스럽게 배우는 숫자이다(오직 사람만이 자연수의 개념을 아는 동물이다). 개수를 알고 난 뒤, 사람이 가장 먼저 배우는 연산이 ‘덧셈’이다. 예를 들어 돌멩이 다섯 개가 있는데, 돌멩이 한 개를 더 가져다 놓으면 전부 몇 개냐는 종류의 지극히 당연한 질문에서 출발한 연산이기 때문이다. 앞서의 질문을 수식으로 표현한 것이 바로 5+1을 구하는 문제이다. 마찬가지로 1+1을 구하라는 것은 돌멩이 한 개에 돌멩이 한 개를 더 가져다 놓을 때 몇 개냐는 질문을 숫자로 쓴 것에 불과하다. 답이 2일 수밖에 없는 것이다.

 

 

그런데 왜 1+1=2를 증명하는 것이 어렵다는 소문이 난 것일까? 이러한 말이 나도는 기원 중의 하나로는 버트런드 러셀(Bertrand Russell, 1872-1970)과 앨프리드 화이트헤드(Alfred Whitehead, 1861-1947)의 ‘수학 원리(Principia Mathematica)’ 라는 책이 꼽히고 있다. 이 책은 수학자들이 보기에도 난해하기 짝이 없는 기호를 동원하여 1+1=2를 증명하는데, 그 증명이 360쪽에 나온다고 (몇 번째 판이냐에 따라 약간의 차이는 있다) 알려져 있다. 그렇긴 하지만 여기에서 간과한 점이 하나 있다. 저 책은 1+1=2 하나만을 증명하기 위해 쓴 책이 아니므로, 앞쪽에 1+1=2의 증명과는 관련이 없는 내용이 아주 많이 들어 있다는 사실이다. 이 책은 이른바 기호 논리학, 집합론을 철저하게 밑바닥부터 구성하기 위해 쓴 책이기 때문에 ‘논리’ 자체와, 집합론, 자연수까지도 최소한의 원리만을 가지고 완벽하게 구성한 다음에야 1+1=2와 같은 사실을 ‘증명’하고 있다. 그러니 그 증명이 한참 뒤에 나올 수밖에 없다. 이 ‘수학원리’는 내용이 거의 기호로 설명되어 있어 읽기가 어렵기로 유명하다. 그래서 실제로 '수학원리'를 다 읽은 사람은 총 세 명, 저자 두 명과 수학자 쿠르트 괴델(불확정성의 정리로 유명하다) 밖에 없다는 전설이 있다.

 

 

 

예전에 모 드라마에서 수학 천재인 주인공이 “페아노 공리계를 이용해서 1+1=2를 증명한다”는 말을 해서 잠깐 화제가 된 적이 있는데, 대체 무슨 뜻일까? 여기에서, 앞서 설명한 1+1=2인 이유를 다시 살펴보자. 엄밀히 따지면 돌멩이를 이용해 ‘설명’한 것이지 ‘증명’한 것은 아니라는 반론이 있을 수 있다. 그렇다면 1+1=2임을 증명하기 위해 하는 수 없이 ‘수학 원리’를 매일 한 쪽씩 1년 동안 읽어야 하는 것일까? (그래도 닷새는 남는다.) 그렇지 않다는 것을 보여주는 대표적인 것이 바로 페아노 공리계이다. 사실 1+1=2는 자연수 ‘1’과 ‘2’가 무엇인지, 자연수의 덧셈 ‘+’가 무엇인지 명확히 해 주는 순간 어이없을 정도로 당연히 증명돼 버린다. 그래서 “이게 뭐야?”라는 소리가 절로 나오는 증명이다. 그러니까 드라마에서 수학 천재를 보여주는 장치로는 적절하지 않다는 얘기다. 아래를 더 읽어보면 알겠지만, 덧셈을 ‘정의’하기 시작하자마자 증명이 나올 것이다. ‘자연수가 무엇이냐’, ‘덧셈이 무엇이냐’를 명확히 정의하는 공리 체계가 여러 개 있는데, 그 중에서도 가장 직관적이고 자연스러워 많이 애용되는 공리 체계는 이탈리아 수학자 주세페 페아노(Giuseppe Peano, 1858-1932)가 고안한 ‘페아노 공리계’이다.

 

 

 

 

 

페아노 공리계가 자연스러운 것은, 사실 사람이 자연수를 배우는 방법인 손가락을 꼽는 방법을 그대로 흉내 내었기 때문이다. 누구나 처음 숫자를 배울 때는 손가락을 꼽는다. 이유도 모르면서 그냥 손가락을 하나 꼽으면서 그것을 1이라고 부른다. 이것을 수학적으로는 “1은 자연수이다”라고 말한다. 그럼 1만 자연수일까? 어린아이는 손가락을 더 꼽으면서 1 다음은 2이고, 2 다음은 3이고, 3 다음은 4이고... 이런 식으로 모든 자연수를 다 배웠을 것이다. 이것을 ‘손가락’같은 용어를 빼고 수학적으로 표현하자면 “n이 자연수이면, ‘n 다음 수’는 자연수이다”가 된다. n 다음 수를 n’ 이라고 쓰기로 하면, 1’ = 2, 2’ = 3, 3’ = 4,… 라고 쓸 수 있다. 한편 1에 대해서는 “n’ = 1인 자연수 n은 없다”가 성립한다. 자연수는 이제 잘 알겠지 싶은 아이에게 숫자를 세어보라고 물어보면, 1, 2, 3, 5,... 같은 식으로 숫자를 한 두 개쯤 건너뛰는 일은 흔한데, ‘3 다음은 5가 아니야’라고 알려주는 사람이 자연수의 개념을 제대로 아는 것이다. 앞서 나온 ‘다음 수’의 용어를 써서 표현하면, ‘3의 다음 수는 4의 다음 수와 다르다’고 쓸 수 있다. 이것을 더 일반적으로 표현하면 “ m과 n이 다르면, m’과 n’도 다르다”가 된다. 이 정도만 알면 자연수는 다 안 것이나 다름없다, 즉, 위의 네 가지 성질을 갖는 가장 작은 것이 바로 자연수라는 것이 이름도 거창한 ‘수학적 귀납법의 원리’이다. 이것을 식으로 표현하면 “ 1 ∈ P이고, 모든 n ∈ P에 대해 n’ ∈ P가 성립하면 P는 자연수 집합을 포함한다(여기서 1 ∈ P라는 것은 1이 P라는 집합에 속한다는 뜻이다)”가 된다. 위의 5가지를 공리로 하여 자연수를 정의한 것을 ‘페아노의 공리계’라고 한다. (참고로 자연수를 0부터 시작하는 경우도 있다. 이 글에서는 원래대로 1부터 시작했음을 밝혀둔다.)

 

 

 

 

 

이제 자연수 집합에서 덧셈 a + b를 정의해 보는데, 이것 역시 처음 덧셈을 배울 때를 돌이켜 보자. 아이들이 머리가 발달하면서 돌멩이 다섯 개에 한 개를 더 놓으면, 굳이 처음부터 세지 않고도 다섯의 다음수가 여섯임을 떠올리고 여섯 개라는 것을 쉽게 알아채는 단계에 이르게 된다. 즉, ‘한 개를 더하면 다음수’라는 얘기인데, 식으로 쓰면 아래와 같다.

 

 

위에서 m=1이면 1 + 1 = 1'가 된다. 그런데 1’을 2라고 부르기로 하였으므로 1+1=2일 수밖에 없다! 다시 말해, “어떤 수에 1을 더하면 다음수인데, 1의 다음수는 2”라는 말이 1+1=2라는 공식의 본질을 담고 있다.   원하는 1+1=2는 증명했지만, 아쉬운 점이 많다. m + 1 = m’은 자연수에 1을 더하는 방법은 가르쳐 주지만 2나, 3 등을 더하는 방법을 가르쳐 주지 않기 때문이다. 그러므로 아직은 3+4=7 같은 것을 증명할 수는 없다. 다시 돌멩이의 비유를 들자. 아직 덧셈을 모르는 아이에게 돌멩이 세 개가 있는 곳에 돌멩이 네 개를 놓으면서, 개수를 물어보면 곧바로 대답하기가 힘들다. 하지만 돌멩이 네 개를 놓을 때 하나씩 천천히 놓으면 얘기가 달라진다. 돌멩이를 한 개 놓으면 개수가 네 개이고, 한 개 더 놓으면 개수가 다섯 개이고,…, 한 개씩 더 놓을 때마다 개수가 전보다 하나 많아진다는 것을 알기 때문이다. 이것을 기호로는 아래와 같이 쓴다.

 

 

이 두 가지 성질만 알면 덧셈은 모두 알게 된다. 좀 더 도전해 보고 싶다면 1+7이 8이라는 것을 증명해 보기 바란다. 7+1=8이라는 것은 이미 설명했다. 하지만 1+7은 7+1과는 약간 다르다. 아직 교환법칙을 증명하지 않았기 때문이다.